UN NUEVO MODO DE HACER MATEMÁTICAS

Un nuevo modo de "hacer" matemáticas

Comparemos el punto de vista de Hilbert en su formalismo geométrico con la teoría kantiana del conocimiento matemático, poniendo especial atención en la teoría de esquemas. En la Crítica de la razón pura, Kant sostiene que es imposible pensar los conceptos geométricos sin darles un objeto: "No podemos pensar en una línea sin trazarla en el pensamiento, ni un círculo sin describirlo, como tampoco representar tres dimensiones del espacio sin construir tres líneas perpendiculares a partir del mismo punto" (B 154). Esta simple observación es un signo indicativo de que el peso de los esquemas geométricos en la epistemología matemática de Kant es superior a lo que aquí he dicho. En efecto, en las secciones precedentes me he referido a los esquemas como instancias que permiten construir en la representación objetos en conformidad con los conceptos. Pero lo dicho por Kant en el pasaje anterior les otorga una mayor importancia: sin esquemas es imposible pensar los conceptos geométricos en absoluto, pues esta actividad precisa una representación interna de ellos.

Lo anterior no constituye ningún problema para Kant, pues, para él, los conceptos geométricos nacen ligados a una forma de representación. Pero, desde la perspectiva que abre el principio de dualidad, este maridaje entre esquemas y conceptos se rompe: las "rectas" pueden ser lo que siempre fueron o lo que originalmente eran los "puntos". Ergo, los conceptos definidos por los axiomas son algo más que los esquemas, poseen una mayor generalidad, con lo que la teoría se descubre como algo más abstracto de lo previsto, como algo que ya no está indisolublemente ligado a un sistema fijo de objetos. De hecho, en la geometría de Hilbert, los conceptos se piensan sin esquemas, aunque hay circunstancias en las que esto no es lo más adecuado para el investigador. Esta disociación entre los conceptos y sus representaciones abrió una feraz posibilidad: pensar la teoría per se, es decir, convertirla en un objeto de estudio.

Esto último lo hace Hilbert en los Grundlagen der Geometrie. Lo que ahí investiga no son los objetos que dice Kant (ciertas entidades construibles en la intuición pura), sino la teoría misma. Digamos que la escudriña primariamente: a ella, no a sus interpretaciones.

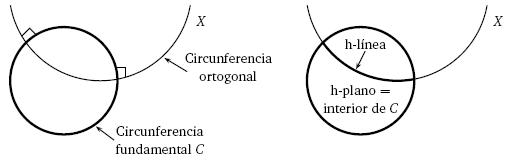
Esta manera de abordar la teoría señala el surgimiento de la teoría de modelos, donde el juego consiste en interpretar los términos y las relaciones fundamentales de distintas maneras.²⁹ En particular, muchos modelos de la teoría geométrica y sus variantes resultan de enlazar sus conceptos con ciertos esquemas. Un notable ejemplo es el modelo de Poincaré para la geometría hiperbólica, en el que al concepto formal de línea se le asocia un esquema euclidiano como sigue. Sea C una circunferencia fija en el plano euclidiano. Si X es una circunferencia que corta ortogonalmente a C, entonces el arco de X que se halla en el interior de C es una h–línea (la "h" con el propósito de diferenciarla de las líneas euclidianas). Aquí, el caso es que contamos con un esquema (euclidiano) para producir circunferencias ortogonales a C, y es a través de este esquema que especificamos las h–líneas del modelo (para una geometría que no es euclidiana).

Este modo de tratar la teoría geométrica significó un desplazamiento en las investigaciones y tuvo importantes consecuencias. Para empezar, permitió una enorme economía de pensamiento: cada proposición demostrada era válida en todos los modelos de la teoría, donde ya no se la tenía que investigar. Y las ganancias no se redujeron a eso. La posibilidad de interpretar la teoría de distintas maneras permitió a Hilbert explorar su conexión con otros dominios de la matemática, con sorprendentes resultados. Por ejemplo, este nuevo tratamiento lo llevó a relacionar los teoremas de Desargues y Pascal con las propiedades de los anillos en el álgebra; v.gr, "Si el teorema de Desargues es válido en un dominio, entonces el álgebra de segmentos es un anillo quizá no conmutativo"; o bien, "El álgebra de segmentos basada en el teorema de Pascal es un anillo conmutativo." Estas investigaciones forman parte de los Grundlagen der Geometrie. Es más, el sentido del trabajo se puede invertir: en vez de ver qué clase de álgebra resulta a partir de un espacio, se pueden "construir" espacios a partir de las álgebras (v.gr., espacios afines a partir de anillos ternarios).

Es evidente que nada de lo anterior habría sido posible si la matemática se hubiera mantenido dentro de los estrechos límites impuestos por el concepto de objeto matemático ofrecido por Kant. Esto lo sabía Hilbert, para quien la investigación axiomática representó un factor de expansión y descubrimiento en esta disciplina.

Podemos decir, entonces, que para Hilbert la axiomática es algo más que un instrumento para ordenar las teorías; más bien, se trata de un medio para la investigación matemática. Esto se advierte claramente en los Grundlagen der Geometrie, donde "jugando" con los axiomas, Hilbert obtiene numerosos resultados: geometrías no arquimedianas, nuevos teoremas acerca de la continuidad, una nueva caracterización topológica del plano, una caracterización de la geometría euclidiana y de la geometría de Bolyai y Lobachevsky mediante grupos de desplazamientos, un análisis del papel de los teoremas de Desargues y de Pascal en la coordenatización del espacio, un estudio comparativo de las distintas geometrías entre sí, y una investigación de los medios requeridos para demostrar ciertos teoremas.

En este sentido, las investigaciones de Hilbert en torno a los fundamentos de la geometría significaron un triunfo para el método axiomático, al punto de que, en su opinión, éste estaba llamado a ocupar un lugar preeminente no sólo en la matemática, sino en la ciencia en general.³⁰